回归框架下的人脸对齐和三维重建

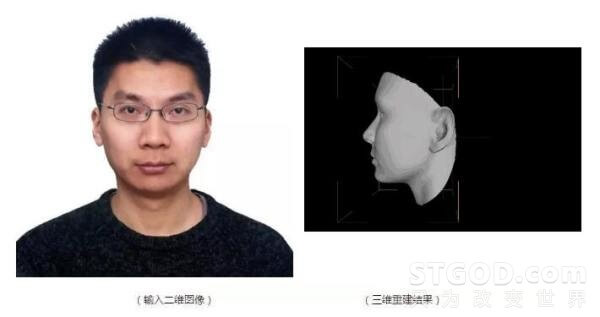
三维人脸重建的目标是根据某个人的一张或者多张二维人脸图像重建出其三维人脸模型（此处的三维人脸模型一般仅指形状模型，定义为三维点云）。

今天我们只讨论由单张二维图像重建三维人脸的问题。这个问题本身其实是个病态（ill-posed）问题，因为在将人脸从三维空间投影到二维平面上形成我们看到的二维人脸图像的过程中，人脸的绝对尺寸（如鼻子高度）、以及由于自遮挡而不可见的部分等很多信息已经丢失。

在不掌握相机和拍摄环境的相关参数的情况下，这个问题其实是没有确定解的。

为了解决这一病态问题，一个直接思路是借助机器视觉中的Shape-from-Shading（SFS）方法。

但是该方法依赖于光照条件和光照模型的先验知识，而未考虑人脸结构的特殊性，在任意拍摄的人脸图像上效果一般。

后来，Kemelmacher-Shizerman和Basri [1] 引入了平均三维人脸模型作为约束条件对传统的SFS方法进行了改进，取得了不错的效果。然而，重建结果往往都接近平均模型，缺少个性化特征。

另一个常用思路是建立三维人脸的统计模型，再将该模型拟合到输入的二维人脸图像上，利用拟合参数实现三维人脸的重建。

这类方法基本都是基于Blanz和Vetter提出的三维形变模型（3D Morphable Model，简称3DMM） [2]。

由于3DMM采用主成分分析（PCA）方法构建统计模型，而PCA本质上是一种低通滤波，所以这类方法在恢复人脸的细节特征方面效果仍然不理想。

此外，上述两类方法在重建过程中对每幅图像都需要求解优化问题，因而实时性较差。

受到近年来回归方法在人脸对齐中的成功应用的启发，我们最早试图建立二维人脸图像上的面部特征点（包括眼角、鼻尖、嘴角等）与人脸三维模型之间的回归关系。

这一思路的基本出发点是面部特征点是反映人脸三维结构的最直观依据。我们尝试根据二维特征点的偏差直接预测三维人脸形状的调整量。

这就好比我们知道二维特征点是由三维人脸形状投影得到的，如果我们发现二维特征点存在偏差，那么根据这一线索我们就应该能够计算出三维人脸形状应该做怎样的调整。

而这个计算过程可以用事先训练好的二维特征点偏差与三维形状调整量之间的回归函数来实现。

基于这样的思路，我们成功地设计实现了在给定输入二维人脸图像上的特征点的条件下实时重建其三维模型的新方法。

相关结果发布在Arxiv [3]。

沿着上述思路，基于2D人脸特征点和3D人脸形状之间很强的相关性，我们进一步尝试将二维人脸图像特征点检测（即人脸对齐）与三维人脸重建过程耦合起来，在回归的框架下同时实现这两个任务。

这就是我们今天要介绍的发表在ECCV2016上的工作 [4] （以下称ECCV2016方法）。扯了这么多（希望不是那么远^_^），下面正式进入正题。

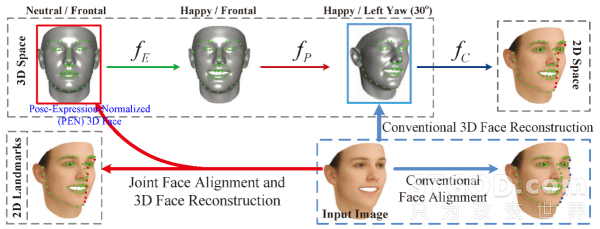
如上图所示，之前研究者大都将2D特征点定位和3D人脸重建两个过程割裂开来解决，而这两个工作本质是一个“鸡生蛋、蛋生鸡”问题。

一方面，2D特征点 U 可由中性3D人脸 S 经过表情（FE ）、姿态变换（ FP）及投影（ FC）得到，即

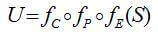
另一方面，2D特征点携带有丰富的几何信息，这也是3D重建方法的基础。

现有的2D特征点检测方法大部分是基于2D人脸形状建模的，主要存在以下几个问题：i）很难去刻画3D平面外旋转的人脸特征点；ii）在人脸姿态不是很大的情况下，通过变化人脸轮廓特征点语义位置来解决自遮挡的情况，这样会导致不同姿态下检测的特征点语义信息不一致 [5]（如上图，人脸图像中蓝色点所示）；iii）在更大姿态下，尤其是yaw方向超过60度以后，人脸区域存在近一半自遮挡，遮挡区域的纹理特征信息完全缺失，导致特征点检测失败。

现有的利用2D特征点来恢复3D人脸形状的方法也存在以下几个问题：i）需要第三方2D特征点检测算法或者手动得到2D特征点；ii）不同姿态下检测的特征点语义信息不一致，难以确定3D点云中与其对应的点 [6]；iii）只生成与输入人脸图像同样姿态和表情的3D人脸，而这样的3D人脸，相对于姿态和表情归一化的3D人脸而言，显然并不有利于人脸识别。

ECCV2016方法的整体框架如下：

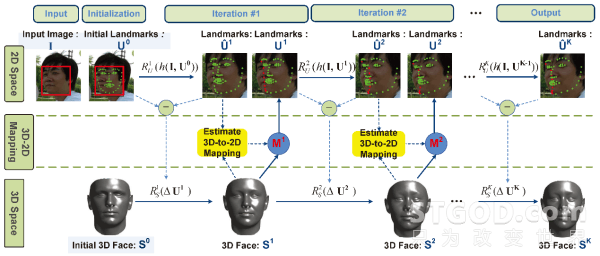
为了在一个框架内处理2D特征点定位和3D人脸重建，我们利用两组级联的线性回归，一组用来更新2D特征点，另一组用来更新3D人脸形状。

在每一次迭代中，先用SDM[7]方法得到特征点更新量，基于方法[3]再用特征点的更新量去估计出3D人脸形状的更新量。新的3D人脸一旦更新就可以粗略地计算出3D-to-2D投影矩阵，同时再利用3D人脸对特征点进行修正，尤其是自遮挡区域的特征点位置及特征点可见性信息。

整个过程2D特征点、3D人脸形状、3D-to-2D投影矩阵的更新都是一个由粗到精的估算过程。

我们先给出利用训练好的回归模型检测任意一张二维人脸图像上的特征点，并重建其三维模型的过程。

值得指出的是：Step 5中，从3D人脸投影得到2D特征点对人脸形状和姿态都有很强的约束。

而Step 2中，特征点是通过纹理特征指导得到的，其中自遮挡区域由于纹理信息的缺失，回归得到的特征点常常是不准确的。通过此步骤3D投影来修正能够有效地提高特征点检测的准确度。

在训练过程中，为了得到上述回归模型，需要提供成对的标定好特征点的二维人脸图像及其对应的三维人脸数据

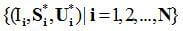
为了更好地处理任意姿态、任意表情的二维人脸图像，训练数据中需要包括尽量多不同姿态和不同表情的人脸，而对应的三维人脸则都是中性表情的、且已经稠密对齐的点云数据。

下面我们重点介绍一下用于人脸对齐的2D特征点回归的目标函数和用于三维人脸重建的3D形状回归的目标函数。

该目标函数建立当前2D特征点周围的纹理特征与其距离真实位置的偏移量之间的回归关系。我们训练所用2D特征点是从3D形状投影得到的，因而确保了语义上的一致性。

同时为了处理大姿态人脸图像，如果某个特征点被判定为不可见点，那这个点的SIFT特征向量置为0。

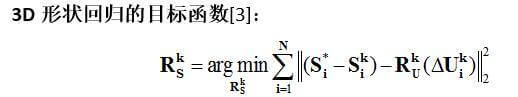
3D形状回归建立的是2D特征点修正量与3D形状修正量之间的关系。

所有训练3D人脸都进行了稠密对齐，且2D特征点之间也作好了对齐，所以并不需要增加额外的平滑约束，同时也尽量保持了3D人脸的个性化差异。训练数据中的3D形状是姿态-表情归一化（Pose and Expression Normalized，简称PEN）3D人脸，如此重建得到的PEN 3D人脸更适用于人脸识别。

在公开测试集上的实验结果证明了在统一的回归框架下同时解决人脸对齐和三维重建的有效性。ECCV2016论文中还进一步证明了重构出来的姿态与表情归一化的三维人脸在提升人脸识别准确率方面的有效性。

最后，我们展示利用ECCV2016方法得到的人脸对齐和三维重建的几个典型结果。

参考文献

[1] Kemelmacher-Shlizerman, I., Basri, R.: 3D face reconstruction from a single image using a single reference face shape. TPAMI (2011).

[2] Blanz, V., Vetter, T.: A morphable model for the synthesis of 3D faces. In: SIGGRAPH (1999).

[3] Liu, F., Zeng, D., Li, J., Zhao, Q.: Cascaded regressor based 3D face reconstruction from a single arbitrary view image. arXiv preprint arXiv:1509.06161 (2015 Version)

[4] Liu F, Zeng D, Zhao Q, Liu X.: Joint face alignment and 3D face reconstruction. In: ECCV (2016).

[5] Jourabloo, A., Liu, X.: Pose-invariant 3D face alignment. In: ICCV (2015)

[6] Qu C, Monari E, Schuchert T. Fast, robust and automatic 3D face model reconstruction from videos. In: AVSS, 113-118 (2014)

[7] Xiong X, De la Torre F. Supervised descent method and its applications to face alignment. In: CVPR. 532-539 (2013)